Koefisiensi korelasi, biasa disebut r, adalah sebuah nilai yang menentukan seberapa kuat hubungan antara 2 variabel. Rumus untuk menghitung koefisien korelasi adalah:
$$ r= \frac{\sum{(x-\overline{x})(y-\overline{y})}}{\sqrt{\sum{(x-\overline{x}})^2 \sum{(y-\overline{y}})^2}} $$Kisaran nilai yang mungkin untuk koefisien korelasi adalah -1,0 hingga 1,0. Artinya, nilainya tidak boleh melebihi 1,0 dan kurang dari -1,0. Angka -1,0 menunjukkan nilai korelasi negatif sempurna dan 1,0 berarti angka korelasi positif yang sempurna. Secara visual seperti yang ditunjukan pada Gambar 1.
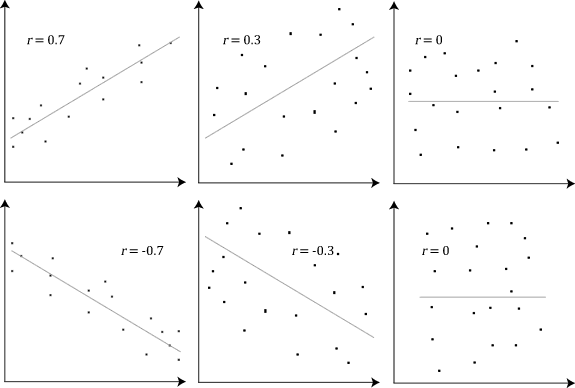
Interprestasi Korelasi
Ada 3 penafsiran hasil analisis korelasi :
- Melihat arah hubungan antar dua variabel
- Melihat kekuatan hubungan antar dua variabel
- Melihat signifikansi hubungan antar dua variabel
Klasifikasi Koefisien Korelasi
Adapun klasifikasi Koefisien Korelasi menurut Jonathan Sarwono adalah:
| Nilai Korelasi | Keterangan |
| r = 0 | Tidak ada korelasi antara 2 variabel |
| 0 < r < 0,25 | Korelasi antara 2 variabel sangat lemah |
| 0,25 < r < 0,50 | Korelasi antara 2 variabel cukup |
| 0,50 < r <0,75 | Korelasi antara 2 variabel kuat |
| 0,75 < r < 0,99 | Korelasi antara 2 variabel sangat Kuat |
| r = 1 | Korelasi antara 2 variabel kuat sempurna |
Contoh Mencari Koefisien Korelasi
Misalkan terdapat 2 data yaitu x dan y, nilai dari kedua saya tersebut adalah
$$ x = 18,16,20,22,26,12,14,20 \\ y = 12,10,8,20,24,10,16,18 $$Hitunglah nilai koefisien korelasinya.
Kode Python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#data
x = [18,16,20,22,26,12,14,20]
y = [12,10,8,20,24,10,16,18]
#membuat dataframe
df = pd.DataFrame(list(zip(x, y)),
columns =['x', 'y'])
df.head()
df.describe()
#rata-rata variabel x
df['x'].mean()
#rata-rata variabel y
df['y'].mean()
Correlation (r)¶
$$ r= \frac{\sum{(x-\overline{x})(y-\overline{y})}}{\sqrt{\sum{(x-\overline{x}})^2 \sum{(y-\overline{y}})^2}} $$Menghitung korelasi menggunakan numpy¶
np.corrcoef(df['x'], df['y'])
Menghitung korelasi secara manual¶
x_mean = df['x']-df['x'].mean()
print(x_mean)
y_mean = df['y']-df['y'].mean()
print(y_mean )
sum_ = np.sum(x_mean * y_mean)
sum_
sqrt_ = np.sqrt(np.sum(x_mean**2)* np.sum(y_mean**2))
sqrt_
correlation = sum_/sqrt_
print(correlation)
plt.title('Korelasi variabel x dan y')
plt.scatter(df['x'], df['y'])
plt.xlabel('x')
plt.ylabel('y')
plt.show()
Hubungan antara variabel x dan y adalah berkorelasi kuat.
Kesimpulan
Jika mengetahui adanya hubungan 2 variabel, maka akan diketahui 1 variabel bisa dilakukan penaksiran terhadap 1 variabel lain, melalui bantuan garis regresi. Korelasi memungkinkan peneliti untuk mempelajari variabel alami yang mungkin tidak praktis untuk diuji secara eksperimental.
Untuk artikel terkait statistik dapat dilihat di sini.





